Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself.[1]
Suppose that j : N → M is an elementary embedding where N and M are transitive classes and j is definable in N by a formula of set theory with parameters from N. Then j must take ordinals to ordinals and j must be strictly increasing. Also j(ω)=ω. If j(α)=α for all α<κ and j(κ)>κ, then κ is said to be the critical point of j.
If N is V, then κ (the critical point of j) is always a measurable cardinal, i.e. an uncountable cardinal number κ such that there exists a <κ-complete, non-principal ultrafilter over κ. Specifically, one may take the filter to be 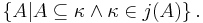 Generally, there will be many other <κ-complete, non-principal ultrafilters over κ. However, j might be different from the ultrapower(s) arising from such filter(s).
Generally, there will be many other <κ-complete, non-principal ultrafilters over κ. However, j might be different from the ultrapower(s) arising from such filter(s).
If N and M are the same and j is the identity function on N, then j is called "trivial". If transitive class N is an inner model of ZFC and j has no critical point, i.e. every ordinal maps to itself, then j is trivial.